Méthodes expérimentales et analyse de données
Projet B (LNG-1100)
1 Introduction
La recherche suivante porte sur l’acquisition du langage par des enfants natifs du français québécois et âgés de 24 mois. Les données utilisées ont d’abord été récoltées dans la base de données Wordbank par Frank et al. (2017) et ont ensuite été adaptées en 2023 pour obtenir celles du projet. L’étude avait comme but principal d’évaluer la capacité de production de mots par les enfants selon, entre autres, la fréquence standardisée des mots en français, leur degré de concrétude et leur classe lexicale. Dans une étude réalisée en 2011 (Kern et Santos (2011)), les chercheurs indiquent que le degré de familiarité d’un enfant vis-à-vis d’un mot a un effet sur l’acquisition de ce mot. Cette familiarité étant souvent intrinsèquement reliée à la fréquence du mot, nous formulons la question suivante : Est-ce que la fréquence des mots a un effet sur la capacité de production des enfants de 24 mois ? En se fiant aux résultats de la littérature, la fréquence a un effet sur la production.
2 Exploration des données
En visualisant les données une première fois, on peut déjà déterminer que les variables prédictives pertinentes pour évaluer la variable binaire de production seraient le sexe du participant, la classe lexicale, la fréquence et le degré de concrétude du mot. Nous avons donc enlevé les colonnes qui ne nous seraient pas utiles, en conservant également l’identifiant du participant et les mots étudiés. Nous avons aussi retiré toutes les lignes dans lesquelles il manquait des valeurs (NA).
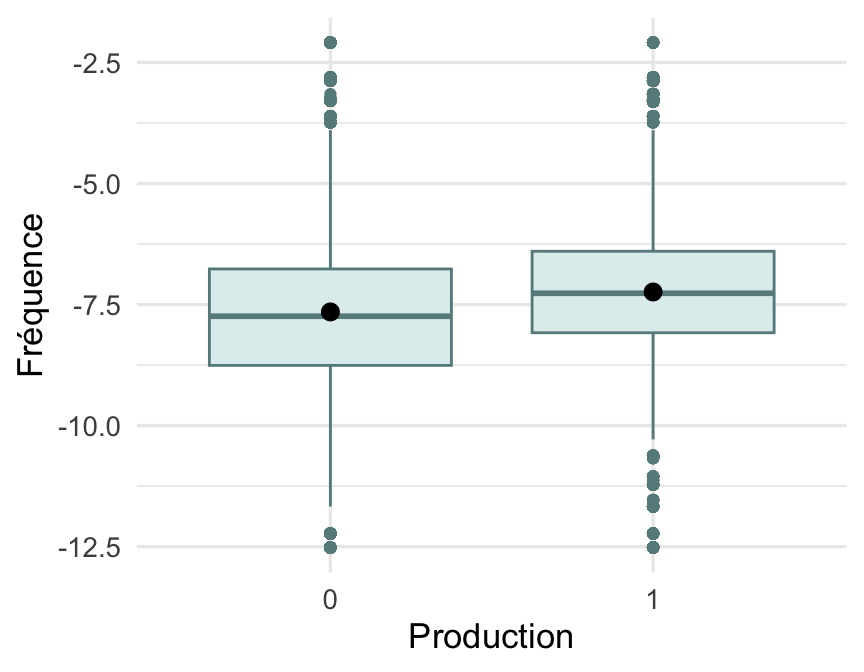
Après analyse sommaire et survol de la littérature (Cauvet et al. (2011), Kern et Santos (2011) et Bassano (1998)), nous avons choisi d’utiliser la fréquence du mot comme variable prédictive, ce qui nous a mené à formuler notre question de recherche. La Fig. 1 illustre l’effet de la fréquence sur la production. À première vue, il semble y avoir des différences visibles entre les moyennes et les médianes des mots prononcés et celles des mots non prononcés. Par contre, des tests statistiques sont requis pour déterminer si ces différences sont significatives ou non.
3 Analyse
3.1 Régression logistique simple
L’hypothèse nulle de notre modèle est que la variable prédictive frequency n’a pas d’impact sur la production des mots par les enfants de 24 mois. Comme mentionné dans la Section 2, la Fig. 1 semble démontrer un effet significatif de la fréquence sur la production des mots dans la langue française. Cet effet peut être confirmé à l’aide de la régression logistique simple, comme le démontre le Tableau 1 : \(\hat\beta\) = 0,15, IC 95% = [0.13, 0.17], p < 0,001.
| produces | |||
| Variables | Coefficients | IC 95 % | Valeur p |
| (Intercept) | 1.38 | 1.25 – 1.52 | <0.001 |
| frequency | 0.15 | 0.13 – 0.17 | <0.001 |
| Observations | 18792 | ||
| R2 Tjur | 0.015 | ||
Il y a une corrélation positive entre l’augmentation de la fréquence et la production des mots (\(\hat\beta\) = 0,15 log-odds). Cela signifie qu’une hausse d’une unité de la fréquence d’un mot augmente de 1,16 les chances que l’enfant le produise. Toutefois, il est important de noter que le \(R^2\) Tjur n’est que de 0,015 et donc que seulement 1,5 % des données peuvent être expliquées par le modèle.
3.2 Régression logistique multiple
Pour vérifier si l’effet de la variable frequency sur la variable produces est toujours significatif, nous avons créé un modèle de régression logistique multiple, en ajoutant la variable concreteness au modèle utilisé à la Section 3.1.
| produces | |||
| Variables | Coefficients | IC 95 % | Valeur p |
| (Intercept) | 0.60 | 0.44 – 0.75 | <0.001 |
| frequency | 0.23 | 0.21 – 0.25 | <0.001 |
| concreteness | 0.33 | 0.30 – 0.37 | <0.001 |
| Observations | 18792 | ||
| R2 Tjur | 0.033 | ||
Selon le Tableau 2, on peut voir que les deux variables ont un effet significatif sur la variable réponse, soit la production langagière. De plus, l’ajout de la variable concreteness dans le modèle montre une augmentation significative de l’effet de la fréquence sur la production, puisqu’il est passé de (\(\hat\beta\) = 0,15, IC 95% = [0.13, 0.17], p < 0,001) à (\(\hat\beta\) = 0,23, IC 95% = [0.21, 0.25], p < 0,001). Avec le nouveau modèle, les chances de produire le mot augmentent de 1,26 pour chaque unité de fréquence, plutôt que de 1,16 comme dans le modèle 1. Le \(R^2\) Tjur est également passé de 0,015 à 0,033, indiquant qu’il est maintenant possible d’expliquer 3,3 % de la variation de la production langagière des enfants de 24 mois. Aussi, l’intervalle de confiance représente le même écart dans les deux modèles, soit de 0,04. Finalement, l’effet de concreteness dans ce modèle est également significatif (\(\hat\beta\) = 0,33, IC 95% = [0.30, 0.37], p < 0,001), ce qui confirme que plus les mots sont fréquents, plus les enfants ont de chances de réussir à produire les mots demandés.
3.3 Prédictions
Pour voir l’effet prévu de la fréquence et de la concrétude sur la production de mots selon notre modèle de régression logistique multiple (voir Section 3.2), nous avons créé la Fig. 2, qui présente la courbe interactive de prédictions. Selon cette figure, plus le mot est fréquent, plus les chances pour un enfant de le produire sont élevées. En effet, un mot dont la fréquence standardisée est de -13,0 a une production prévue de 1,08 %, alors qu’un mot dont la fréquence est de 12 aurait une production de 99,5 %. Dans l’intervalle sélectionné de fréquence, soit [-30, 30], la production minimale est inférieure à 0,002 % et la production maximale est d’environ 100,0 %. Lorsque la fréquence est [-7, 4], la pente est plus grande, signifiant que la production augmente de façon plus importante. On remarque que la courbe atteint un plateau minimal et maximal et que, même si elle s’en approche beaucoup, la production ne peut atteindre exactement 0 % ou 100 %.
4 Conclusion
Pour conclure, l’hypothèse initiale est confirmée par les résultats de nos modèles. Effectivement, ces derniers démontrent un effet significatif de la variable frequency sur la variable produces. Cependant, en vertu de l’importance de la variation individuelle dans le processus d’acquisition (Kern (2003)), la variable prédictive n’explique pas un taux élevé de réponses. En observant le \(R^2\) Tjur, on constate que la partie expliquée est minime, soit de 1,5 % à 3,3 %. Cette conclusion pourrait être due au fait que toutes les valeurs de la variable frequency sont moins fréquentes que la moyenne, donc les données ne sont pas assez réparties; l’étude réalisée ne permet pas d’observer l’effet des mots ayant une fréquence au-dessus de la moyenne. Il serait intéressant, dans des recherches ultérieures, d’avoir un ensemble de données comportant des mots plus fréquents dans la langue française afin d’analyser l’effet de cette variable de façon plus complète.
Notes
Pour plus d’informations sur les fonctions utilisées, consulter Barnier (2023). Toutes les figures et les graphiques ont été conçus avec R Core Team (2023).
Références
Barnier, Julien. 2023. « Introduction à R et au tidyverse ».
Bassano, Dominique. 1998. « L’élaboration du lexique précoce chez l’enfant français: structure et variabilité ». Enfance 51 (4): 123‑53.
Cauvet, É, P Brusini, I Brunet, et A Christophe. 2011. « Comment les enfants apprennent leur langue maternelle: LE MOT JUSTE: Comment le cerveau l’acquiert, le choisit et le produit ». Pour la science (Imprimé), nᵒ 403: 42‑49.
Frank, Michael C, Mika Braginsky, Daniel Yurovsky, et Virginia A Marchman. 2017. « Wordbank: An open repository for developmental vocabulary data ». Journal of child language 44 (3): 677‑94.
Kern, Sophie. 2003. « Le compte-rendu parental au service de l’évaluation de la production lexicale des enfants français entre 16 et 30 mois ». Glossa, 48‑61.
Kern, Sophie, et Christophe dos Santos. 2011. « Input et acquisition du lexique en français: rôle de la fréquence et de la densité de voisinage ». Travaux de didactique du français langue étrangère, nᵒ 65-66: 53‑70.
R Core Team. 2023. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.